Die Methode des Persistenzindex (PX)
(Der folgende Text ist in veränderter Form nach SCHÜTZ 2008, Seiten 51-55 zitiert)
Bislang existieren keine Verfahren, die einen objektiven und nachvollziehbaren Weg zur Erfassung und Bewertung von persistenten (historischen) Grundrissstrukturen in Städten eröffnen. Ebenso fehlen bislang die dazu notwendigen, quantitativen Methoden und damit verbundene Kenngrößen. Mit der Methode des Persistenzindex wird dies erstmals möglich. Der Index ist einfach, aussagekräftig und objektiv (unabhängig von individuellen, subjektiven Einstellungen bzw. Einflüssen).
Zur Operationalisierung der Messung von persistenten Strukturen im Stadtgrundriss müssen sich diese Strukturen durch bestimmte Merkmale präzise beschreiben und in messbare Tatbestände, also Indikatoren fassen lassen. Messbare Tatbestände stellen im Fall von Parzellarstrukturen deren Lage im Raum und deren physische Grenzen, also in der Regel Länge und Breite der Parzelle dar. Länge und Breite lassen sich sehr genau bezüglich ihrer Lage und Ausdehnung (Länge) im Raum bestimmen. Durch Bestimmung von Lage und Ausdehnung zu verschiedenen Zeitpunkten und dem Vergleich der Ergebnisse lassen sich diese Strukturen präzise beschreiben. Aus den Ergebnissen lässt sich der Persistenzindex ableiten, der angibt, in welchem Ausmaß sich Parzellarstrukturen im Grundriss erhalten haben.
Bezüglich der (wissenschafts-)theoretischen Zuordnung des Konzeptes des Persistenzindex und der entwickelten Methoden innerhalb bereits vorhandener Konzepte der Geographie lässt sich der Persistenzindex neben der Zugehörigkeit zum Konzept der Persistenz von seinem Aufbau her in die "zentrale Kategorie" der Dichte nach LICHTENBERGER (1998, S. 87, S. 96-100) einordnen. Der Flächen- bzw. Raumbezug wird dabei im Verhältnis der geographischen Objekte zur Fläche definiert, wie dies z.B. bei der von LICHTENBERGER angeführten Gebäudedichte (Zahl der Gebäude/ ha) der Fall ist. Neben einem zentralen Konzept zur Beschreibung einer Stadt weist LICHTENBERGER auch auf die Verwendung der Dichtewerte als "normatives Instrument" im Städtebau und in der Stadtplanung hin (LICHTENBERGER 1998, S. 96). Der Persistenzindex (PX) erfüllt also zum einen die Anforderung des Raumbezugs durch die Ausweisung von persistenten Strukturen pro Flächeneinheit (z.B. pro Baublock), zum anderen kann er als Instrument in Städtebau und Stadtplanung verwendet werden. Folgt man nun der Feststellung von LICHTENBERGER (1998, S. 96), dass die Dichte in der Stadtgeographie bislang kaum beachtet wurde, so leistet der Persistenzindex auch einen Beitrag zum "Forschungsdesiderat" der Untersuchung der Kategorie der "Dichte" in Städten.
Dieser "Dichte-Ansatz" von LICHTENBERGER war nicht neu, sie folgt damit im Wesentlichen NYSTUEN. Dieser hat die Dichte als "von fundamentaler Wichtigkeit" (NYSTUEN 1963, hier: 1970, S. 93) für eine geographische Betrachtungsweise bezeichnet. LICHTENBERGER wendet den allgemein gefassten "Dichte-Ansatz" von NYSTUEN allerdings auf städtische Räume an, weshalb der Persistenzindex primär der "zentralen Kategorie" der Dichte nach LICHTENBERGER und nicht nach NYSTUEN zuzuordnen ist.
Erste Vorschläge zur Anwendung des Persistenzindex in der Geographie wurden von PLÖGER in seiner Dissertation gemacht. Er schlägt vor, den PX für die Überprüfung von Vektordaten und von Straßenverläufen anzuwenden (PLÖGER 2003, S. 152, 168, 180). Bezüglich einer derartigen Anwendung des Persistenzindex z.B. für die Altstraßenforschung kann beispielsweise der Frage nach persistenten Strukturen bezüglich von Relikten römischer Straßenverläufe nachgegangen werden.
BENDER und JENS ziehen die Anwendung des Persstenzindex für "Strukturen (z.B. Parzellengrenzen, anthropogene Geländekanten, Waldränder etc.) oder Objekte/Landschaftselemente" (BENDER, JENS 2004, S. 41-42) in Betracht. Sie wollen aus dem Persistenzindex einen "historisch-geographischen Strukturwert (HGS)" ableiten. Dieser könnte eine Maßzahl für die "kulturhistorisch bedingte Schutzwürdigkeit" von Landschaftselementen (BENDER, JENS 2004, S. 42) darstellen.
Der Persistenzindex in der Geographie - formale Darstellung/Definition
Der Persistenzindex besteht aus drei Teilen:
PX = f(K1 .. Kn); (Z1 - Z2)a, Z2 in konkreter Ausprägung z.B.: 1; 192a, 1811
Der erste Teil des Index "f(K1 .. Kn)" kann dabei Werte von 0 bis 1 annehmen. "f(K1 .. Kn)" steht für die Funktion zur Berechnung der Übereinstimmung von räumlichen Strukturen. Im Ergebnis ergibt sich eine prozentuale Angabe zur Übereinstimmung der untersuchten Objekte innerhalb einer bestimmten Fläche. Im objektorientierten Ansatz wird über das Attribut der Zeit berechnet, welche Zahl von Objekten, die immer durch eine Folge von Koordinaten(paaren) dargestellt werden, in einem bestimmten Zeitraum persistent geblieben sind.
Der Zweite Teil des Index "(Z1 - Z2)a, Z2 gibt den Zeitraum an, für den räumliche Strukturen auf Übereinstimmung getestet werden. Z1 und Z2 stellen dabei feste Zeitpunkte bzw. Zeitschnitte dar, das kleine a bedeutet, dass diese Zeitpunkte Jahresangaben darstellen. Z2 stellt immer den "älteren" Zeitpunkt dar, so dass die Differenz Z1 - Z2 eine Maßzahl für die Dauer der Persistenz darstellt (z.B. Z1 = 2003, Z2 = 1811, Z1 – Z2 = 2003 - 1811 = 192). Je größer diese Maßzahl, desto länger ist die Persistenz belegt. Diese Maßzahl ist immer positiv oder gleich null. Bei Jahresangaben vor Christi Geburt ist der Jahreszahl ein Minus voranzustellen. Diese Maßzahl ist sinnvoll, da sich Untersuchungen zur Persistenz fast ausnahmslos auf zwei zu vergleichende Zeiträume beziehen. Unten wird ein Beispiel für mögliche Werte des PX und deren inhaltliche Aussage gezeigt.
Die ursprüngliche Methode zur Berechnung des Persistenzindex (SCHÜTZ 1999) war abhängig von der Abweichung zweier Geraden, da sie von einem layer-orientierten Ansatz ausging. Es wurden dort zwei Geraden in zwei unterschiedlichen Ebenen verglichen. Aus dem Grad der Übereinstimmung dieser Geraden wurde der PX berechnet. Die Berechnung erfolgte über den Satz des Pythagoras. Die vorgenannte Art der Berechnung ist jedoch mit folgenden Problematiken verbunden: Falls die zulässige Abweichung der zu vergleichenden Geraden zu gross gewählt wird, werden in der Realität nicht übereinstimmende Geraden für übereinstimmend erklärt. Falls der Abstand zu klein gewählt wird, werden Ungenauigkeiten in den Quellen (Karten) als Abweichungen in der Realität gesehen. Diese Berechnung des Persistenzindex kann also nur zur Anwendung kommen, falls absolut fehlerfreie Bedingungen vorliegen. Dies ist in der Regel jedoch nicht der Fall.
Eine erste Verbesserung des Persistenzindex stellte die Beschränkung auf die Analyse von Geraden mit lediglich zwei sehr genau vermessenen Punkten (Anfangs- und Endpunkt der Geraden) und gleicher Länge dar. Dadurch werden die (Teil)Geraden direkt vergleichbar (HÄUBER, SCHÜTZ 2001, S. 232). Doch auch diese Methode kann nur beim Vorliegen sehr genau vermessener und geprüfter Datenbestände angewandt werden. Die Datenbestände müssen zudem vor dem Vergleich komplett in teilweise sehr kurze Geraden(teile) mit zwei Punkten aufgeteilt werden. Eine "einfache" Anwendung und Übertragung auf beliebige Datenbestände ist in beiden Berechnungsarten des Persistenzindex nicht möglich, da im ersten Fall die Abweichungen und Toleranzwerte zunächst mit aufwendigen Verfahren ermittelt werden müssen, im zweiten Fall umfangreiche Aufbereitungen notwendig sind. Dies kann in der Regel nur von Personen durchgeführt werden, die mit den zu analysierenden Karten bzw. Katastern und zudem mit der Methoden geographischer Informationsverarbeitung bestens vertraut sind. Ein weiteres Problem dieser Berechnung des PX ergibt sich bezüglich der Bezugsgrößen. Dort werden nämlich absolute Längen miteinander verglichen. Der PX will aussagen, welche Anzahl "historischer" Strukturen persistent sind, d.h. noch vorhanden sind (vgl. HÄUBER, SCHÜTZ 2001, S. 234). Dafür wurde die Anzahl aller Längen von Parzellengrenzen in einem Baublock auf die Anzahl der Längen bezogen, die aus älteren Karten bzw. Katastern noch vorhanden sind.
Beispiele für Werte des Persistenzindex (PX) und deren Bedeutung
|
Wert des PX |
Aussage |
Fallbeispiel |
|
1;192a,1811 |
Das untersuchte Objekt (Punkt, Linie, Fläche) ist innerhalb eines Zeitraumes von 192 Jahren völlig persistent. Es wurde das 1811 existierende Objekt untersucht. |
Eine Parzelle hat ihre Grenzen zwischen den Jahren 1811 und 2003 nicht verändert. Vgl. Abbildung unten links (Parzellen 158 und 159). |
|
0;192a,1811 |
Das untersuchte Objekt (Punkt, Linie, Fläche) ist innerhalb eines Zeitraumes von 192 Jahren völlig verschwunden. Es wurde das 1811 existierende Objekt untersucht. Der Wert 0 kann jedoch auch bedeuten, dass das untersuchte Gebiet 1811 noch nicht parzelliert gewesen ist. |
Eine Parzelle aus dem Jahre 1811, oder Teile ihrer Begrenzung sind im Kataster von 2003 nicht mehr verzeichnet. Vgl. Abbildung unten rechts (sämtliche Parzellen aus dem Jahre 1811 sind verschwunden). |
Bedeutung von Werten des Persistenzindex
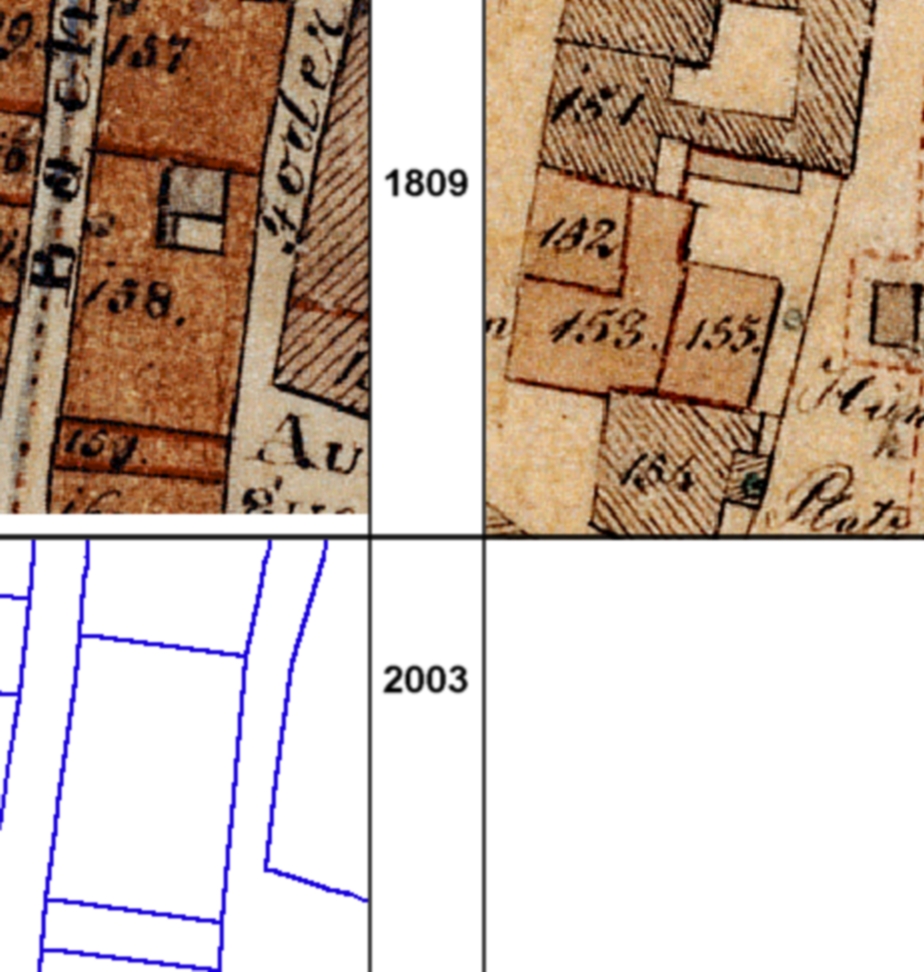
Links: Parzellen 1811 Nr. 158, 159 in der Bachgasse in Regensburg (über 192 Jahre persistent).
Rechts: Parzellen 152, 153, 155 am St. Georgen Platz in Regensburg (Persistenz = 0).
Quellen: Bay. Landesvermessungsamt 2008 (Uraufnahme 1811), Stadt Regensburg 2008 (StGK 2003).
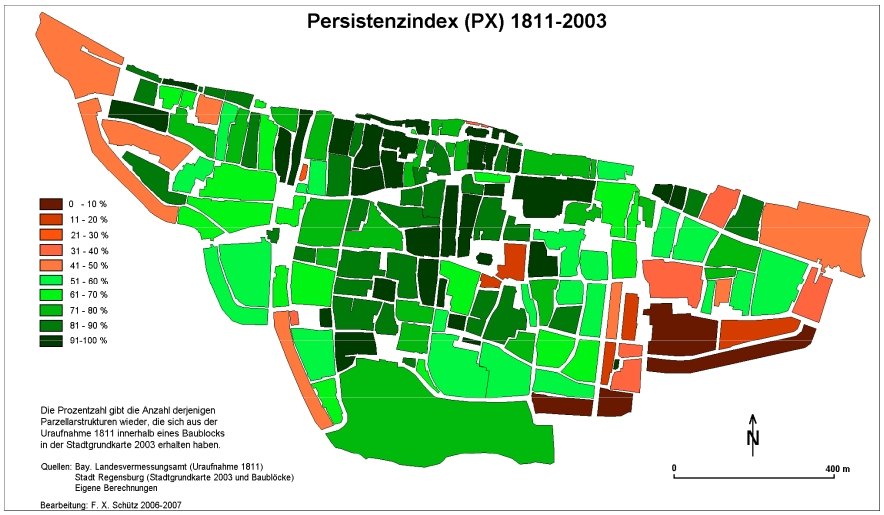
Karte mit Darstellung des Persistenzindex für die Stadt Regensburg (Beilage 6 aus SCHÜTZ 2008)
Anmerkung:
Der Begriff Persistenzindex existiert zudem in folgenden Fachgebieten, was der Autor allerdings 1998 - zum Zeitpunkt, als er die Idee hatte, die hier betrachtete wissenschaftliche Problemstellung als "Persistenzindex" zu benennen - (noch) nicht wusste:
Persistenzindex in der Tierzucht, Biometrie und theoretischen Populationsgenetik, vgl. zum Beispiel "Persistenzindex" (SCHNEEBERGER 1978, Seite 12).
Persistenzindex in der Informatik, vgl. zum Beispiel "Persistent Index" (HON, LEE, SADAKANE, TSAKALIDIS 2013).
Persistenzindex in der Meteorologie, vgl. zum Beispiel "weather persistence index (WPI)" (HOFFMANN, LEHMANN, FALLAH, HATTERMANN 2021).
Zitierte Literatur
BENDER, O., JENS, D. (2004): Zur Qualität der "historischen Kulturlandschaft" - Diachronische Landschaftsbewertung auf Vektordatenbasis. In: STROBL, J., BLASCHKE, T., GRIESEBNER, G. (Hrsg.): Angewandte Geoinformatik 2004. Beiträge zum 16. AGIT-Symposium Salzburg. Heidelberg. S. 35-44.
HÄUBER, Chrystina, SCHÜTZ, Franz Xaver (2001): The Analysis of Persistent Structures - a Functionality of the Archaeological Information System FORTVNA. In: STROBL et al. (Hrsg.): Angewandte geographische Informationsverarbeitung XIII. Beiträge zum AGIT-Symposium Salzburg 2001. Heidelberg. S. 227- 237.
HOFFMANN, Peter, LEHMANN, Jascha, FALLAH, Bijan, HATTERMANN, Fred F. (2021): Atmosphere similarity patterns in boreal summer show an increase of persistent weather conditions connected to hydro-climatic risks. Scientific Reports | (2021) 11:22893 | https://doi.org/10.1038/s41598-021-01808-z
HON, Wing-Kai, LEE, Lap-Kei, SADAKANE, Kunihiko, TSAKALIDIS, Konstantinos (2013): Compressed Persistent Index for Efficient Rank/Select Queries. In: LNCS, Volume 8037, Seiten 402-414.
LICHTENBERGER, Elisabeth (1998): Stadtgeographie. Begriffe, Konzepte, Modelle, Prozesse. Band 1. 3., neu-bearb. u. erw. Aufl. Stuttgart, Leipzig.
NYSTUEN, J.D. (1963): Identification of Some Fundamental Spatial Concepts. In: Papers of the Michigan Academy of Science, Arts, and Letters, Bd. 48. S. 373-384. (Hier wurde die Dt. Übersetzung in BARTELS (1970) unter dem Titel: "Die Bestimmung einiger fundamentaler Raumbegriffe" verwendet).
PLÖGER, Rolf (1999): Anwendung Geographischer Informationssysteme (GIS) für historisch-geographische Aufgabenstellungen. In: EBELING, D. (Hrsg.): Historisch-thematische Kartographie: Konzepte - Methoden - Anwendungen. Bielefeld. S. 9-23. (Anm. zum Beitrag auf S. 197-198).
SCHÜTZ, Franz Xaver (1999): GIS-gestützte Analyse von persistenten Strukturen in der Kölner Innenstadt auf der Basis der Kataster von 1836/37, 1938/39, 48 und dem aktuellen Kataster. Unveröffentlichte Diplomarbeit, Universität Bonn, Geographische Institute.
SCHÜTZ, Franz Xaver, HÄUBER, Chrystina (2001): Reconstructing Ancient Rome using Remote Sensing and GIS-Technology: The Archaeological Information System FORTVNA. In: JÜRGENS, C. (Hrsg.): Remote Sensing of Urban Areas/ Fernerkundung in Urbanen Räumen. (RGS, H. 35). S. 91-92; S. 283-294 (auf beiliegender CD).
SCHÜTZ, Franz Xaver (2008): Zum Regensburger und Kölner Stadtgrundriss. Eine GIS-gestützte Untersuchung. Regensburg (= Regensburger Studien Band 14, herausgegeben vom Stadtarchiv Regensburg).
SCHNEEBERGER, Markus (1978): Der Verlauf der Laktationskurve und die Schätzung der Milchleistung beim schweizerischen Braunvieh. ABHANDLUNG zur Erlangung des Titels eines Doktors der technischen Wissenschaften der EIDGENÖSSISCHEN TECHNISCHEN HOCHSCHULE ZÜRICH. Zürich.