Franz Xaver Schütz
Motivation
Geodaten in einem Archäologischen Informationssystem (AIS) liegen in der Regel in einem bestimmten Koordinatensystem vor. Im Fall des AIS ROMA handelt es sich beim Referenzdatensatz um photogrammetrische Daten, die uns freundlicherweise seit 1999 von der Comune di Roma (aktuell Roma Capitale) zur Verfügung gestellt wurden1. Diese amtlichen Daten liegen im Koordinatensystem Gauss-Boaga vor. Bei der Integration von Daten und bei Rekonstruktionen im 2/3/4D-Bereich liegen die Grunddaten, Karten, Pläne, Zeichnungen und weitere Quellen in der Regel aus unterschiedlichen Zeiträumen in unterschiedlichen Genauigkeiten, Koordinaten-systemen und Projektionen vor. Von besonderer Bedeutung sind dabei die Himmelsrichtungen und die Orientierung in einem räumlich-temporalen Bezugssystem, für die unterschiedliche Meridiane, Koordinatensysteme und Projektionen existieren.
Mit diesem Beitrag will ich aus Sicht der Geowissenschaften und der Geo-Medieninformatik die Begrifflichkeiten im Kontext der Integration von Daten in ein AIS an einem Beispiel im Marsfeld in Rom ordnen und erklären. Vieles wird die Leserin und der Leser schon einmal gehört oder gelesen haben, häufig ist das Wissen jedoch nicht (mehr) präsent. So schrieb Georg JENSCH 1970 (S. 7) in seinem Vorwort: "daß das Wissen um die Erde als ein Himmelskörper wie ihre Darstellung im Kartenbild zum unentbehrlichen Rüstzeug eines Geographen gehört. Die Überzeugung wurde - auch beim Verfasser - in dem gleichen Maße bestärkt, wie einerseits die Geographie sich anschickte, dieses Wissen zu vernachlässigen ... So ist dieses Manuskript entstanden aus offenbar gewordenen Mängeln mit dem Ziel, Abgetanes wieder zu beleben". Diese Zeilen von JENSCH haben - nach meinen eigenen Erfahrungen in Forschung und Lehre - nichts an Aktualität verloren.
Meridiane
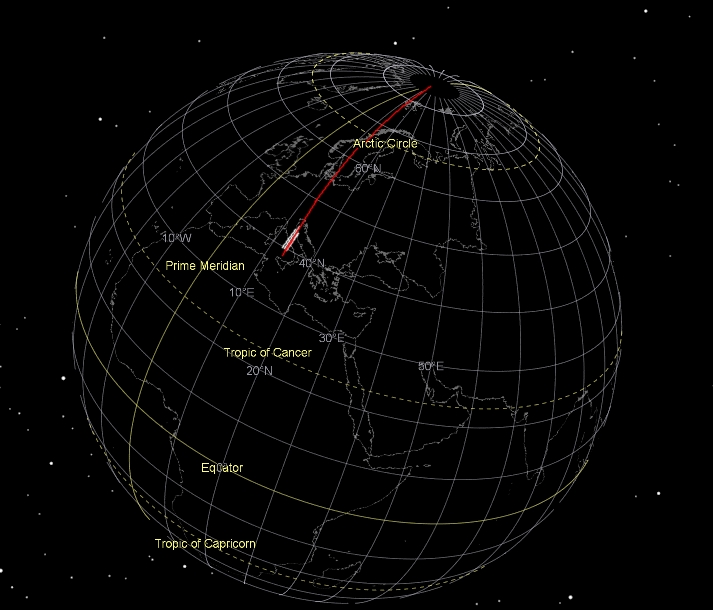
Mittags fällt der Schatten der Sonne genau nach Norden. Die Sonne kulminiert dann, erreicht also ihren höchsten Stand. "Alle Orte, an denen die Sonne zur selben Zeit kulminiert, kann man durch eine Linie verbinden, die man Meridian ( = Mittagslinie) nennt. Bezieht man diese Linie auf die Erde, nennt man sie Ortsmeridian" (WAGNER 1971, S. 19). Durch die Pole der Erde, die "als Punkte auf der Erde mit der Rotationsgeschwindigkeit null" (JENTSCH 1970, S. 40) definiert sind, lassen sich Kreise legen, die als Längenkreise oder Meridiane bezeichnet werden (vgl. Abb. 1). Die Meridiane laufen immer von Norden nach Süden oder von Süden nach Norden.

Abb. 1: Gradnetz der Erde mit Meridianen (Längenkreisen) und Breitenkreisen
(Der rote, vom Nordpol ausgehende Teilmeridian und die damit verbundene, kleine weiße Fläche zeigen den Meridian und die Lage der Abb. 3,4,6 und 7 in starker Vergrößerung; erstellt mit Esri ArcGlobe vom Autor)
Um die Richtungswinkel mit absoluten Zahlen zu bezeichnen, wird ein Meridian als Nullmeridian festgelegt. Bei ihm beginnt die Zählung. Seit dem Jahr 1884 ist der Meridian, der durch die alte Sternwarte von Greenwich läuft international als "Nullrichtung der Längenzählung anerkannt" (SCHÖDLBAUER 2000, S. 157), in Abb. 1 ist er in englischer Sprache als "Prime Meridian" bezeichnet.
Die Längenkreise werden vom Nullmeridian ausgehend 180° in östliche und 180° in westliche Richtung gezählt. In Abb. 1 beispielsweise mit 10°E, was 10° östlicher Länge bedeutet, E steht für East, also Osten. Die östliche oder westliche Länge in Bezug auf Greenwich wird auch als geographische Länge bezeichnet, der Winkel mit dem Zeichen λ.
Neben den Meridianen lassen sich, ausgehend von den beiden Tangentialebenen an den Polen Parallelkreise konstruieren, die auch Breitenkreise genannt werden. Sie werden vom Äquator (in Abb. 1 englisch mit "Equator") aus ( 0°) bis 90° nach Norden und 90° nach Süden gezählt. Der Abstand eines Breitenkreises vom Äquator wird als geographische Breite und mit dem Winkel ϕ bezeichnet. Auf Abb. 1 beispielsweise "20°N", also von der Äquitorialebene aus 20° in Richtung geographischer Nordpol, zu sehen direkt unter der Bezeichnung "Tropic of Cancer" (Wendekreis des Krebses). Die geographische Länge lässt sich heute auch recht genau durch den Unterschied der jeweiligen Ortszeit zur Greenwichzeit bestimmen. Die Erde dreht sich in 24 Stunden einmal um sich selbst, also um 360°. 24 geteilt durch 360 ergibt 0,066666 Stunden pro Längengrad und 0,066666 Stunden entsprechen 4 min. Ist es beispielsweise in Greenwich 12:00 Uhr Mittags (Ortszeit) und unsere Uhr würde 11:00 Uhr Ortszeit zeigen, befänden wir uns 60 Zeitminuten von Greenwich entfernt, als [Korrektur: also] 60 Zeitminuten durch 4° = 15. Wir befinden uns dann also auf dem 15ten Längengrad. Mit der wahren Ortszeit lässt sich auf einfache Weise mit einem genauen Chronometer, der auf Greenwichzeit eingestellt ist, der Längengrad bestimmen.
Wie kann nun die "wahre Ortszeit" bestimmt werden? Seit der Antike dienten und dienen Sonnenuhren dazu, die wahre Ortszeit anzuzeigen. Bereits in der Antike war es offensichtlich sehr schwierig, Sonnenuhren so zu bauen, dass sie selbst am selben Ort die "richtige" Ortszeit anzeigen, wie ein Zitat von Seneca belegt: "facilius inter philosophos quam inter horologia conveniet" (Seneca, Apokolokyntosis, 2.2-3). Ich wurde durch ROHR (1982, S. 18) auf dieses Zitat aufmerksam, wo er schreibt: "In Rom standen Skaphen im Ruf einer ständigen Ungenauigkeit, was vielleicht auf ihr kleines Format, eher aber wohl auf die Leichtfertigkeit und ungenügende Fachkenntnis der Hersteller zurückzuführen war. Der Übergang von sphärischen zu konischen Uhren mag das Ablesen der Zeit erleichtert haben, die Qualität des Zifferblatts hat er nicht gehoben. Bedeutsam ist in diesem Zusammenhang ein Ausspruch, den Seneca getan haben soll, wonach zu seiner Zeit zwei gleichdenkende Philosophen leichter zu finden waren als zwei gleichlaufende Sonnenuhren". Dies bezieht sich insbesondere auf kleinere Sonnenuhren. Bei größeren Sonnenuhren handelt es sich häufig um "Bodensonnenuhren". Diese behandelt beispielsweise SCHUMACHER (1978, ab S. 114). Dabei weist er ausdrücklich darauf hin, dass bei der Konstruktion einer Bodensonnenuhr mit einem Obelisken "der Fuß des Obelisken nicht mit dem konstruktiven Zeigerfußpunkt identisch ist" (SCHUMACHER ebd. S. 116). PEITZ nennt noch den speziellen Typ der analemmatischen Sonnenuhr, die auch azimutale Sonnenuhr genannt wird. Der Zeiger ist nicht erdachsparallel, sondern senkrecht auf einer horizontalen Ebene angebracht. (vgl. PEITZ 1978, S. 68). Die Vorteile einer Sonnenuhr fasst er so zusammen: "Eine Sonnenuhr braucht nicht aufgehalten, nachgestellt oder aufgezogen zu werden, denn sie ist immer so genau, wie der Gang der Sonne. Von der Technik Gottes angetrieben läuft sie ohne menschliche Hilfe bis in die Ewigkeit" (PEITZ 1978, S. 8).
Weil heute meist nicht mehr die "wahre Ortszeit (WOZ)" (SCHUMACHER 1978, S. 50), die dem "wahren örtlichen Mittag" (ebd.) entspricht, angezeigt wird, sondern z.B. in München und Rom in der Regel Mitteleuropäische Zeit (MEZ) bzw. Mitteleuropäische Sommerzeit (MESZ), weicht die von Sonnenuhren angezeigte Zeit in der Regel von unseren Uhren ab, falls diese auf Mitteleuropäische Zeit eingestellt sind. SCHUMACHER (1978, S. 51) beschreibt dies zutreffend so: "Allerdings wird die Mehrzahl der armbanduhrentragenden Betrachter kritisierend feststellen, daß die Sonnenuhr »falsch« geht. Dabei geht - auf den Ort bezogen - die Armbanduhr »falsch«!" Eine triviale Tatsache, die mir jedoch auch erst durch die Arbeit an diesem Manuskript in ihrer ganzen Tragweite klar wurde. Weiter schreibt SCHUMACHER (1978, S. 67): "Noch zu Goethes Zeiten wäre diese Kritik nicht möglich gewesen. Was die Sonnenuhr zeigte, war »wahre Ortszeit«, sie galt. Auch die mechanischen Uhren auf den Kirchtürmen wurden nach ihr gerichtet." Schuhmacher weist zudem darauf hin, dass die verschiedenen Ortszeiten der Kirchturmuhren in einem Land natürlich insbesondere mit der Einführung von festen Fahrplänen für die Eisenbahn nicht mehr tragbar war. Daher wurde für "Mitteleuropa als Standard-Meridian" (ebd., S. 51) der 15. Längengrad Ost maßgebend. Die Stadt Görlitz liegt beispielsweise auf diesem Längengrad (Zählung nach Greenwich 0°) und wenn es dort 12 Uhr Mittag ist, ist auch für alle anderen Ort der Mitteleuropäischen Zeitzone 12 Uhr Mittag. Die Zeitzeichen werden durch Sender verbreitet, deren Reichweite bis zu 2000 km beträgt und lassen sich beispielsweise durch Funkuhren empfangen (ebd., S. 406-407). Der Unterschied zu Greenwich beträgt genau eine Stunde, vgl. oben die Rechnung zum Längengrad bei einer Zeitstunde Unterschied.
Nach SCHÖDLBAUER (2000, S. 374) ist die MEZ 1893 in Deutschland als Gesetzliche Zeit eingeführt worden. Die Grenzen sind der Meridian bei 7,5° und der bei 22,5°, als 15°±7,5°, bezogen auf den Nullmeridian durch Greenwich. "Eine Sommerzeit (Daylight Saving Time)" ist nach SCHÖDLBAUER (2000, S. 378) "erstmals im ersten Weltkrieg in Großbritannien eingeführt worden", ebenso in den Vereinigten Staaten, wie STRAHLER (1973, S. 36) schreibt: "Daylight saving time was adopted in the United States during the First World War, and by act of Congress was put into effect from the last Sunday in April to the last Sunday in September of 1918". SCHÖDLBAUER weist auch darauf hin, dass die Polbewegung der Erde die "Ergebnisse astrogeodätischer Breiten-, Längen- und Azimutbeobachtungen unmittelbar" beeinflußt (ebd. , S. 408). Es existieren zudem viele weitere nationale und internationale Nullmeridiane, also Längenkreise. Seit 1634 war der Meridian von Kap Orchilla ("Kap Ferro") an der Westspitze der Kanareninsel Ferro der am meisten verwendete Nullmeridian. Er stellte damals den westlichsten Punkt der alten Welt dar. (vgl. SCHÖDLBAUER 2000, S. 157). Auch Monte Mario ist ein bedeutender Nullmeridian (vgl. unten).
Neben dem geographischen Nordpol ist auch der nördliche Himmelspol von Bedeutung, der durch den Polarstern festgelegt wird. Die Stellung des Polarsterns hat sich seit der Antike verändert. Durch die Ellipse der Erdbahn um die Sonne wird nämlich eine "Ebene bestimmt, die als Ekliptik bezeichnet wird." (JENSCH 1970, S. 33). Die Bedeutung von Ekliptik ist Finsternislinie, da eine Sonnen- und Mondfinsternis nur auftreten können, wenn die Bahn des Mondes die Ekliptik durchläuft (ebd., S. 33, Fußnote 2). Die Schiefe der Ekliptik im Jahr 1967 wird von Jensch mit 23° 26' 36,87" (JENSCH 1970, S. 32) angegeben. Die Einteilung der Ekliptik erfolgte bereits im Altertum mit den Sternbildern des Tierkreises in zwölf Abschnitte zu je 30°, die in der Summe wieder 360° ergeben. In diesen Tierkreiszeichen findet sich auch der Polarstern. In diesem Zusammenhang spielt auch die Präzession eine Rolle. "Die Präzession verändert den Richtungswinkel der Erdachse in der Ekliptikebene um jährlich nur 50,26", d.h. in ca. 26 000 Jahren hat sie den Kegelmantel einmal voll umschrieben" (JENSCH 1970, S. 37). Als Folge der Präzession stimmen die aktuellen Markierungen von Tag- und Nachtgleiche nicht mehr mit den Sternbildern in der Antike überein. Das Frühlingsäquinoktium ist aktuell im Sternbild der Fische zu finden, zu Hipparchs Zeiten (um 190 v. Chr. bis 125 v. Chr. vgl. SCHÖDLBAUER 2000, S. 615) befand es sich im Sternbild des Widder (ebd., S. 163). Der aktuelle geographische Nordpol weist heute zu dem uns bekannten Polarstern, das tat er jedoch früher nicht. Um 3000 v. Chr. wies er auf den hellsten Stern des Drachens, wie chinesische Angaben bezeugen. Vor 13000 Jahren wies er auf die Wega in der Leier, und die Wega wird in 13000 Jahren von heute wiederum Polarstern sein (vgl. THIEL 1956, S. 13-14). Dies ist in Abb. 2 dargestellt. Durch die Präzession "rückt etwa alle 2000 Jahre der Frühlingsanfang, die Tag- und Nacht-Gleiche im März um ein Tierkreiszeichen weiter. "Im Laufe eines Platonischen Jahres von 25770 Sonnenjahren" werden also "alle Sternbilder durchlaufen" (SCHÖDLBAUER 2000, S. 163).
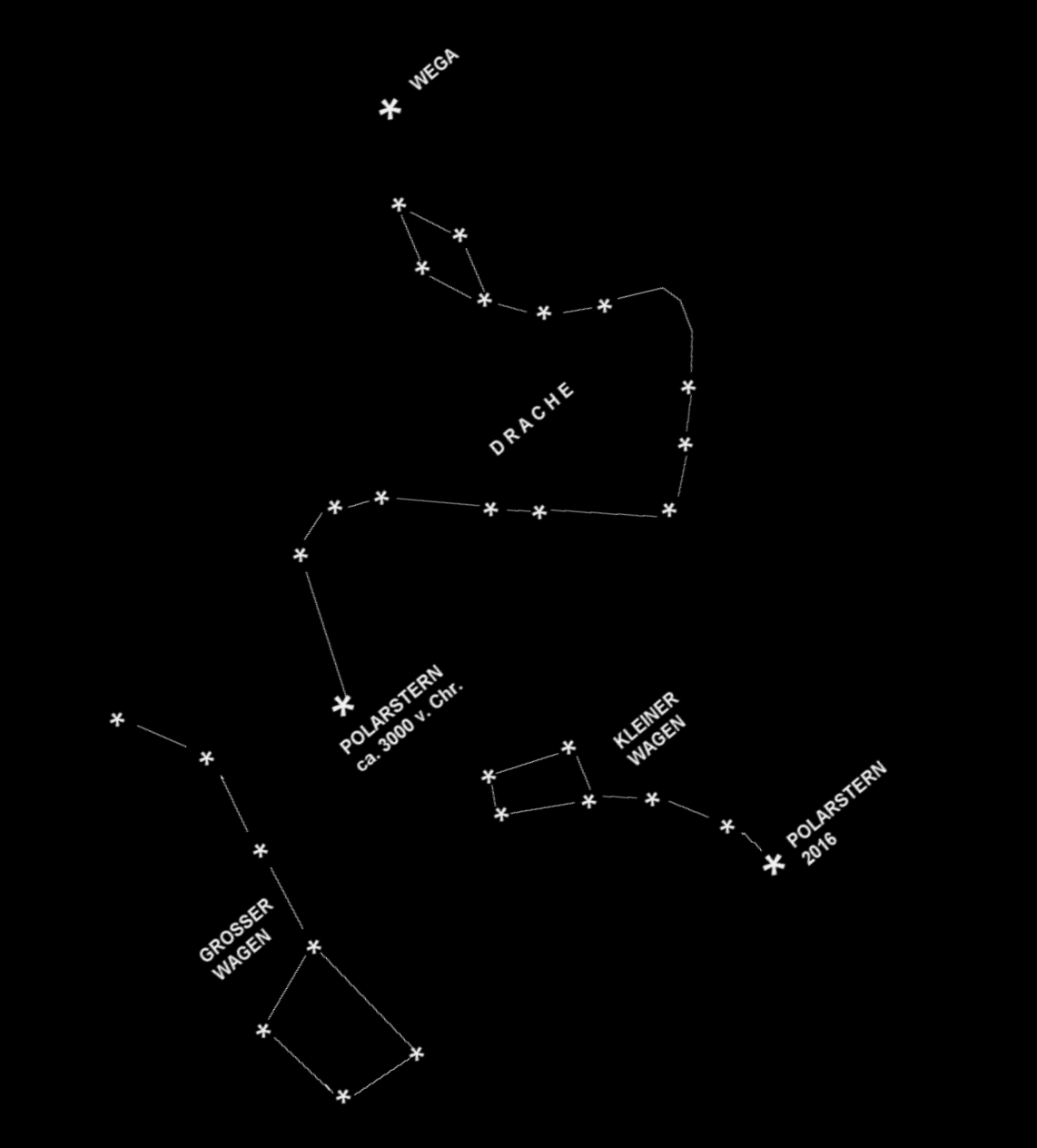
Abb. 2 : Veränderung des Polarsterns
(Zeichnung vom Autor, stark verändert nach THIEL 1956, Abb. 2, S. 14)
THIEL bezeichnet die Veränderung des Himmelspols als "Polwanderung im Lauf der Jahrtausende". Um 4300 v. Chr. wechselte der Sonnenstand am Frühlingsanfang von den Zwillingen in den Stier, um 2100 v. Chr. vom Stier in den Widder und um 100 n. Chr. vom Widder in die Fische. In Abb. 2 steht der Polarstern heute im Vergleich zur Antike östlicher. Um 15.000 n. Chr. wird WEGA Polarstern sein. THIEL sieht dabei auch kulturgeschichtliche Zusammenhänge, dass man beispielsweise "die Stier-Verehrung in Babylon, Ägypten, Kreta damit in Zusammenhang bringen" kann (THIEL 1956, S. 14).
Will man nun den Versuch unternehmen, Ausrichtungen von Gebäuden bzw. anderen Objekten in der Antike zu rekonstruieren, sollte für valide Rekonstruktionen diese Polwanderung in Verbindung mit den verschiedenen Nord-Richtungen (Gitter-, geographisch- und magnetisch Nord, (engl. "grid north, true north, magnetic north", vgl. unten) beachtet werden. Der Himmelspol müsste dazu für die zu rekonstruierende Zeit exakt bestimmt werden. Nach Abb. 2 würde dieser in zurückliegenden Zeiten und, bezogen auf den aktuellen Stand des Polarsterns, in westlicher Richtung liegen. Da der Polarstern aktuell recht genau in geographische Nordrichtung weist, würde dies beispielsweise für Objekte, die in der Vergangenheit - zumindest bis 3000 v. Chr. - nach dem Himmelspol (Himmelsnord) ausgerichtet waren, bedeuten, dass diese Objekte in aktuellen, nach geographisch Nord ausgerichteten Karten etwas nach Westen orientiert sein müssten.
Damit sind wir bei der Orientierung angelangt. Sonne, Mond und Sterne bildeten in der Vergangenheit die einzige Möglichkeit der Orientierung und Orientierung heißt "nach Osten ausrichten" (THIEL 1956, S. 16). Osten und Westen waren die anfänglichen Himmelsrichtungen, dort wo die Gestirne auf- und untergehen. Nach THIEL führte zum Begriff Norden erst die Beobachtung, "daß nicht alle Sterne auf und untergehen, sondern sich in einer bestimmten Himmelsgegend im Kreis drehen" (THIEL 1956, S. 16). Die sieben hellen Sterne, an denen dies besonders zu beobachten war, nannten die Römer "Siebenochsen" (THIEL ebd.) und den Kreismittelpunkt den Norden. Das Sternbild kennen wir heute als den Großen Wagen oder Großen Bären (vgl. Abb. 2). Weiter schreibt THIEL (1956, S. 17): "Die Orientierung nach den Himmelsrichtungen war ein Staatsproblem von höchstem Rang. Für jede Stadt mußte die genaue Lage des Himmelspols ermittelt werden, jeder Tempel, jedes Bauwerk, jedes Grab mußte haargenau nach Norden ausgerichtet sein, der Kaiserthron, der Hausherrensitz, die Haupttür streng nach Süden weisen". Bezüglich der Richtungen hatte man sich in der Antike insbesondere auch nach der Richtung der Winde gerichtet, die durch Windrosen dargestellt wurden (vgl. unten zu "Himmelsrichtungen, Windrosen und Nordpfeile").
Koordinatensysteme
Um Karten anzufertigen, die ein "verkleinertes, gewöhnlich verebnetes, graphisch umgesetztes, generalisiertes Bild" (JENSCH 1970, S. 51) eines Teils der Erdoberfläche, in unserem Fall also der Stadt Rom zeigen, ist ein entsprechendes Bezugssystem notwendig, das grundsätzlich durch ein Koordinatensystem gegeben sein kann. Dies könnten geographische Koordinaten sein (vgl. oben und Abb. 1), es existiert jedoch eine Vielzahl von weiteren Koordinatensystemen. Durch die Problematik einen gekrümmten Teil der Erdoberfläche in einer Kartenebene abbilden zu wollen, lassen sich in einer Karte nie Flächen-, Winkel- und Längentreue gleichzeitig erreichen. Da es sich bei den hier betrachteten Karten und mit dem AIS ROMA erzeugten Karten um Karten mit großem Maßstab handelt, können wir die Erdkrümmung im Grunde vernachlässigen. Allerdings sind verschiedene Projektionen von analogen und digitalen Kartendaten bzw. die Koordinatensysteme und Projektionen, mit denen die Daten erfasst wurden, zu beachten, um keine falschen Karten und damit falsche Visualisierungen von Ergebnissen zu erhalten. Für die Stadt Rom sind Koordinaten im Format Gauss-Boaga von besonderer Relevanz, da sie - nach wie vor - im zivilen, amtlichen Bereich zur Anwendung kommen.
Seit 1923 wurde in Deutschland eine von C.F. GAUSS und von L. KRÜGER vervollständigte Meridianstreifenabbildung eingeführt (JENSCH 1970, S. 89), die "Prof. Boaga" für Italien entsprechend umgerechnet hat (vgl. unten). Diese Abbildung ist winkeltreu. Längen und Flächen werden in zunehmendem Abstand vom Hauptmeridian leicht verzerrt, in unserem Fall, also bei Darstellungen innerhalb eines vergleichsweise "kleinen" Gebietes (im Vergleich zu Ländern und Kontinenten) ist die Verzerrung allerdings vernachlässigbar gering. Als Gradnetz wird ein rechtwinkliges Koordinatennetz benutzt (vgl. auch Abb. 3,4,6) mit einem regelmäßigen Gitter. Jeder Punkt ist durch die Angabe von kartesischen Koordinaten bestimmbar. Der Rechtswert (Abzisse) läuft parallel zum Hauptmeridian und der Hochwert (Ordinate) entspricht der Entfernung vom Äquator.
Seit 1886 ist das italienische Kataster entstanden und die damals benutzte Projektion für diese Karten war Cassini-Soldner (MUGNIER 2005, S. 889). 1945 hat "Prof. Boaga" nach MUGNIER (2005, S. 890) die originalen Gleichungen von C.F. Gauss speziell für die italienische Halbinsel umgerechnet. Das Gitter basiert auf einem Datum, das für Italien während des Zweiten Weltkriegs neu berechnet wurde und "Roma 1940" genannt wurde. Der Datumsursprung ist das "original castle at Monte Mario, where Ф 0 = 41° 55' 25.51" N ±0.027" and Л 0 = 00° 00' 00" = 12° 27' 08.40" East of Greenwich, and with an azimuth to Monte Soratte where: α 0 = 06° 35' 00.88" ±0.12". The ellipsoid of reference is the Hayford 1909 (International 1924) where a= 6,377,388 m and 1/f = 297. The Gauss-Boaga Transverse Mercator (mapping equations are published in the ASPRS Manual of Photogrammetry, 5 th edition), is comprised of two zones: West Zone(I) from 6° to 12° 27' 08.40" East of Greenwich (meridian of Monte Mario), and East Zone (II) from 11° 57' 08.40" (meridian 30' West of Monte Mario) to 18° 30' East of Greenwich." (MUGNIER 2005, S. 890). Mugnier weist zudem darauf hin, dass nach dem zweiten Weltkrieg das Datum für Militärkarten auf ED50 verändert wurde, im zivilen Bereich wurde jedoch weiterhin Roma 1940 angewandt. Er weist zudem darauf hin, dass, selbst falls Koordinaten in geographische Koordinaten mit beispielsweise Datum ERTS89 transformiert werden, immer mit Ungenauigkeiten zwischen 3 bis 4 Metern zu rechnen ist. Dies bedeutet, dass bei der Integration genauer Katasterdaten z.B. in google maps oder andere topographische Karten immer mit Lagefehlern von 3 bis 4 Metern gerechnet werden muss. Für wissenschaftlich genaue Karten und Pläne und darauf basierende Rekonstruktionen sollte daher immer die entsprechende Projektion, hier Gauss-Boaga Transverse Mercator in Verbindung mit den in diesem Koordinatensystem vorliegenden amtlichen Daten benutzt werden. Dies ist beim AIS ROMA seit 1999 der Fall. Zur konformen "Abbildung des Erdellipsoids in die Ebene durch Gauß-Krüger-Meridianstreifen" vgl. auch ausführlich das gleichnamige Kapitel bei WITTE, SPARLA 2015, S. 22-25.
Die Richtung der Gitterlinien des Koordinatengitters bei Gauss-Boaga wird mit "Gitternord" (WITTE, SPARLA 2015, S. 28) bezeichnet. Sie läuft beim Bezugs- bzw. Hauptmeridian genau nach geographisch Nord, bei westlich und östlich des Hauptmeridians gelegenen Gitterlinien weicht sie um einen bestimmten Winkel ab. Dies ist deutlich auf Abb. 3 zu erkennen. Das Gauss-Boaga Gitter ist dort in grüner [Korrektur: roter] Farbe dargestellt, das geographische Gitter mit Meridianrichtung geographisch Nord in roter [Korrektur: grüner] Farbe Dieser Winkel wird als "Meridiankonvergenz γ bezeichnet" (WITTE, SPARLA 2015, S. 28). Diese Meridiankonvergenz ist in Abb. 3 als Abweichungswinkel zwischen den Meridianen des Gauss-Boaga Gitters in grüner [Korrektur: roter] Farbe und den Meridianen des geographischen Gitters in roter [Korrektur: grüner] Farbe deutlich wahrnehmbar. Zu der Thematik "Gauß-Krüger und universale transversale Mercatorprojektion" vgl. auch ausführlich bei BILL 2016, S. 185-187. Bei sehr genauen Berechnungen, beispielsweise im Bereich von Metern fällt die Abweichung deutlich ins Gewicht und sollte entsprechend beachtet werden. Dies trifft etwa bei der Berechnung von Sonnenuhren zu, falls dazu unterschiedliche Koordinatensysteme und Projektionen als Datengrundlagen verwendet werden. Entsprechende Transformationen sind unerlässlich, um zu wissenschaftlich validen Ergebnissen zu kommen.
Ausführlich werden in FLACKE et al., ausgehend von der Frage "Warum liegen die Punkte nicht da, wo sie sein sollten?" (FLACKE et al. 2015, S. 14) und unter Anwendung von ArcGIS 10.2.1 praktische Beispiele und typische Fragestellungen zu Koordinatensystemen, Projektionen und Transformationen für ein Geographisches Informationssystem erläutert. Es wird auch der Begriff Transformation genauer erklärt, der in unserem Zusammenhang wichtig ist. Es wird unterschieden in Umrechnung, die in ArcGIS "projection" genannt wird und in Umformung, die in ArcGIS "geographic transformation" genannt wird (FLACKE et. al. 2015, S. 21). Durch die Projektion werden die Koordinaten einer Ellipsoidoberfläche in ebene Koordinaten umgerechnet, z.B. in unserem Fall von geographischen Koordinaten in "Gauss-Boaga Koordinaten". Eine Umformung bezeichnet eine Datumstransformation, wobei das Datum Bezugsellipsoid, Zentralpunkt, Orientierung und Maßstab bezeichnet (FLACKE et al. 2015, S. 22). Die in ArcGIS verwendeten Parameter für Gauss-Boaga sind beispielsweise unten im Appendix zu finden.
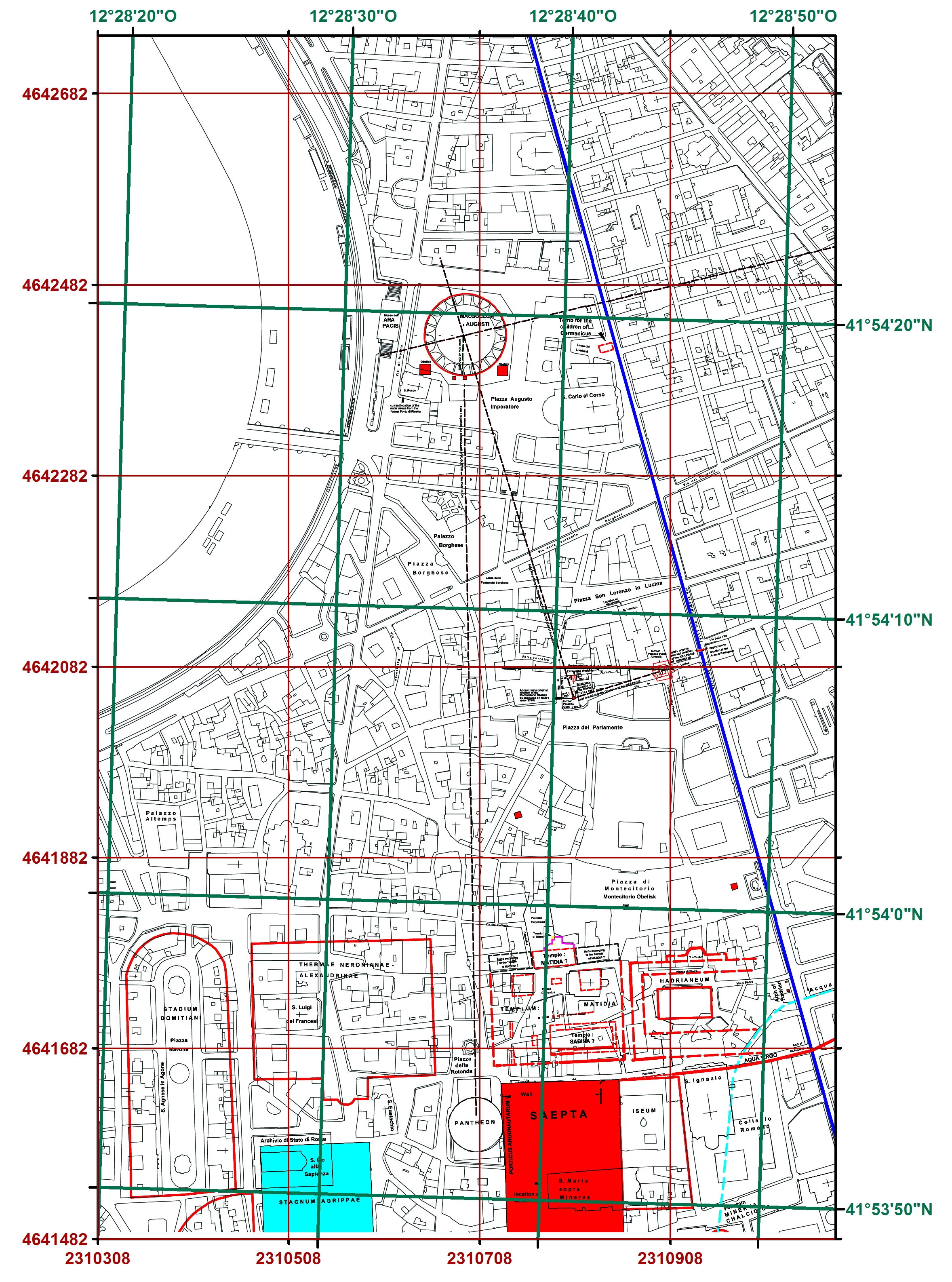
Abb. 3: Gitter mit Gauss-Boaga und geographischen Koordinaten
(Gauss-Boaga Gitter in roter Farbe, geographisches Gitter in grüner Farbe. Die Meridiankonvergenz, also die Abweichung von Gauss-Boaga Gitternord zu geographisch Nord ist deutlich erkennbar. Winkeltreue Abbildung. Grundkarte: Chrystina Häuber, in diesem Band Fig. 3.8 (Detail). Darstellung: Autor, kartographisch nicht überarbeitet)
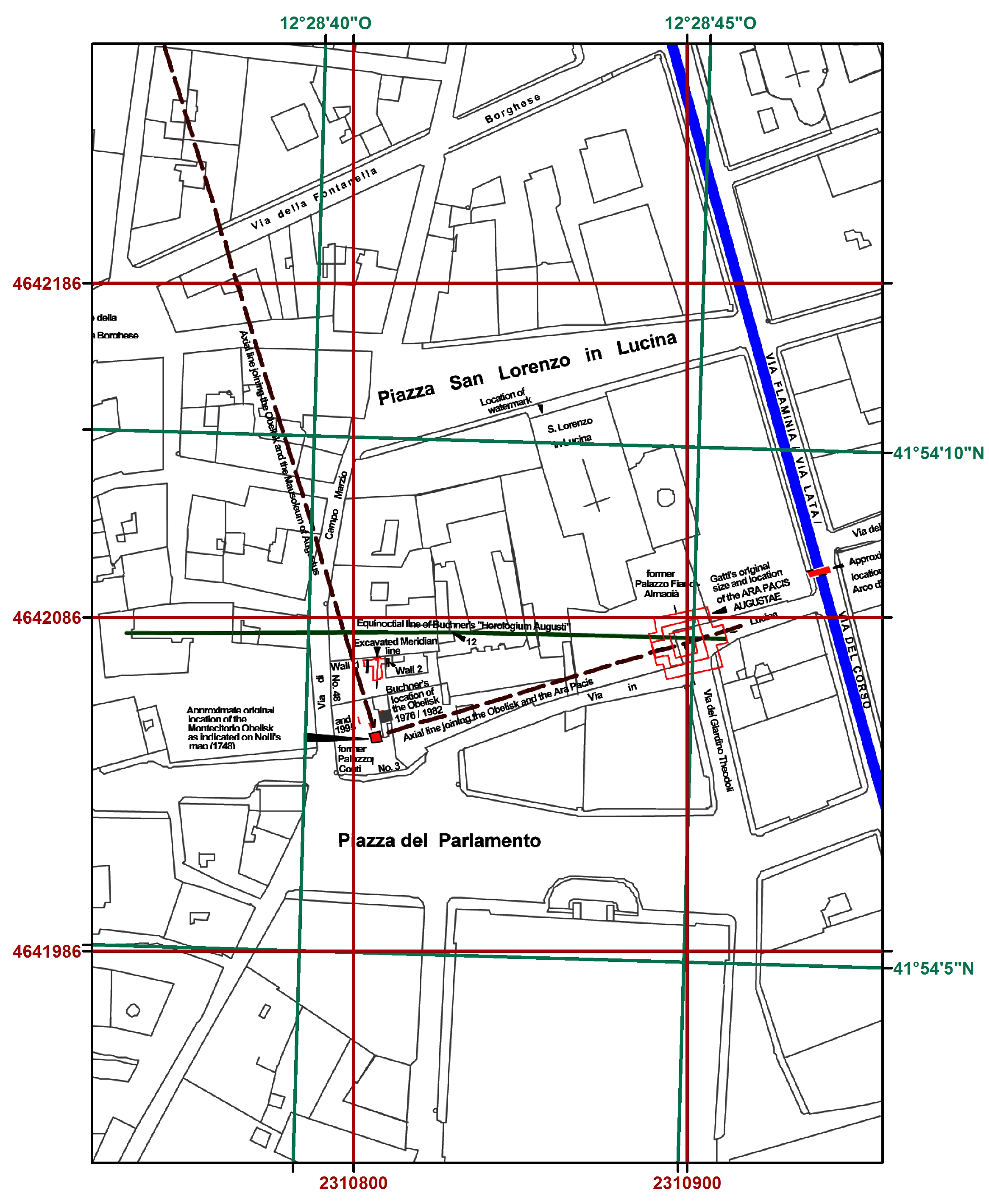
Abb. 4: Gitter mit Gauss-Boaga und geographischen Koordinaten
(Detail aus Abb. 3. Winkeltreue Abbildung. Grundkarte: Chrystina Häuber, in diesem Band Fig. 3.8 (Detail). Darstellung: Autor, kartographisch nicht überarbeitet)
Auf Abbildung 4 sind zwei gestrichelte Linien zu sehen, die zum einen den in der Karte von Nolli eingezeichneten Sockel des Obelisken mit dem Mittelpunkt des Mausoleums des Augustus verbinden und zum anderen mit einer Lokalisierung der Ara Pacis des Augustus. Die gestrichelten Linien bilden bei Messung im hier verwendeten Koordinatensystem Gauss-Boaga Roma 1940 Est in transversaler Merkatorprojektion einen Winkel von 90°. Da diese Abbildung winkeltreu ist, sollte der gemessene Winkel dem tatsächlichen Winkel auf dem Erdellipsoid entsprechen (vgl. oben).
Himmelsrichtungen, Windrosen und Nordpfeile
Norden wird heute auf Karten in der Regel mit einem Nordpfeil gekennzeichnet oder sind mit Gittern "genordet", vgl. oben Abb. 3 und 4. Das war nicht immer so, wie die beiden Windrosen aus der Karte von Falda (1676) und Nolli (1748) in Abb. 5 zeigen.
|
G.B. Falda 1676 |
G.B. Nolli 1748 |
Abb. 5: Windrosen auf historischen Karten
Die Windrosen zeigen die Himmelsrichtungen an und es existiert eine Vielzahl von wissenschaftlichen Untersuchungen zu Windrosen. Zu Windrosen in der Antike vgl. beispielsweise KAIBEL 1885. Zur Orientierung historischer Karten vgl. GULLIVER 1908. Durch "Digitalisierung - Verortung - Recherche" erlebt historisches Kartenmaterial augenblicklich völlig "neue Perspektiven" (vgl. Aufsatz von CHRISTOPH, AMMON, CROM, PRZIBYTZIN 2016) und für den Versuch, räumlich-temporale Modellierungen, Rekonstruktionen und darauf basierende Simulationen zu unternehmen, ist historisches Kartenmaterial unerlässlich. GULLIVER 1908 schreibt auf Seite 56: "The first map showing both true and magnetic north was made in 1530".
Magnetisch Nord
Neben geographisch Nord und Gitternord existiert noch eine weitere Nordrichtung: magnetisch Nord. Bezüglich des Begriffes von "magnetisch Nord" erinnere ich mich gerne an eine Exkursion in meinem Nebenfach Mineralogie, geleitet von Professor Klaus Vieten (1932-2014), an der ich während meiner Studienzeit an der Universität Bonn teilnehmen konnte. Es ging ins Siebengebirge auf den Drachenfels. Der dort anzufindende Trachyt enthält Sanidinkristalle (vgl. RÖSLER 1991, S. 603, 605). Diese Sanidinkristalle sind teilweise mehrere cm groß und polarisiert. Als das flüssige Gestein an die Erdoberfläche kam, "schwammen" diese Kristalle wie Kompassnadeln in der flüssigen Masse und erstarrten letztendlich in einer nach dem damaligen Erdmagnetfeld ausgerichteten Richtung. Professor Vieten wies uns Studierende an, den mitgebrachten Kompass in Richtung der Einsprenglingen anzulegen und wir konnten eine eklatante Abweichung der Polarisierung der Kristalle von der aktuellen Richtung der Magnetnadel zum magnetischen Nordpol sehen. Offensichtlich hatte sich also der magnetische Nordpol der Erde zwischenzeitlich in seiner Lage sehr verändert.
Diese Tatsache wurde lange Zeit wenig beachtet, vgl. WYLLIE (1971): "The discovery by B. Brunhes in 1906 that some rocks are magnetized in a direction opposite to that of the Earth's present magnetic field received very little attention for many years". In seinem Kapitel "Paleomagnetism, polar Wandering, and Spreading Sea Floors" geht WYLLIE (1971, S. 269-305) ausführlich auf die Veränderungen des Magnetfelds der Erde ein. Erstmals kartiert wurde die Feldstärke des Erdmagnetismus von Halley. "Halley bemerkte, daß die Kompaßnadel nicht nach Norden zeigt, daß der Magnetpol mit dem geographischen nicht zusammenfällt (THIEL 1956, S. 190). Nach Halley ist übrigens der Halleysche Komet benannt. Er hat in Seekarten Deklinationskurven eingezeichnet, die Sternkarten des Altertums mit den Ständen der Sterne seiner Zeit verglichen und herausgefunden, dass diese seit Hipparch ihren Platz am Firmament verändert haben. "Die Richtweisung des Kompasses beruht auf den Kraftlinien des magnetischen Erdfeldes" (WAGNER 1971, S. 22). Eine freibewegliche Kompassnadel richtet sich nach den Feldlinien dieses Magnetfeldes aus. Zu unterscheiden ist dabei die horizontale Achse, die Inklination und die vertikale Achse, die Deklination, also die Abweichung von der Nord-Süd-Richtung, sie wird auch Mißweisung genannt. Die Magnetpole stimmen nicht mit den geographischen Polen, also den Polen, die durch die Erdachse definiert werden überein. WAGNER (1971, S. 23) gibt beispielsweise für die Lage des arktischen Magnetpols 1903 nach Amundsen an: ϕ = 70° 30' N; λ = 95° 30' W und für 1950: 70° 40' N; 90° 5' W und für den antarktischen Magnetpol nach der ersten englischen Antarktisexpedition: ϕ = 72° 41' S; λ = 156° 25' O und für 1950: 72° S; 155° O. In lediglich 47 Jahren ist eine deutliche Lageänderung der Magnetpole sichtbar.
In Abb. 6 ist diese magnetische Deklination für Rom mit ihrem aktuellen Wert dargestellt. "Weicht die Nadelachse gegenüber dem geographischen Meridian nach Osten ab, spricht man von östlicher oder positiver, im anderen Fall von westlicher oder negativer Deklination" (MURAWSKI 1977, Lemma "Deklination", S. 36-37). Der aktuelle Wert der Deklination für Rom beträgt nach WMM 2015 (World Magnetic Model für 2015) ca. +2,90°. Die Kompassnadel neigt sich also in östliche Richtung mit einer augenblicklichen Veränderung von ca. 0,11° pro Jahr. Der aktuelle Wert ist auf Abb. 6 als "magnetisch Nord" mit einer Magnetnadel visualisiert. Über die NOAA (National Oceanic and Atmospheric Administration) sind Berechnungen und ein "Download" von Daten des WMM in gängigen Geodatenformaten möglich, auch für den Zeitraum von 1590 bis 2015.
Vgl. https://www.ngdc.noaa.gov/geomag/declination.shtml [aufgerufen am 20.9.2016], unter "Download Historic Maps". Allerdings erfolgt dort auch der Hinweis: " Since there were not many regular observations of the geomagnetic field prior to the 20th century, it is difficult to make a reliable geomagnetic field model for dates before 1900. Based primarily on magnetic data from ship logs, the GUFM model (Jackson et al., 2000, Four centuries of geomagnetic secular variation from historical records, Phil. Trans. Roy. Soc. Lond. A, 358, 957- 90.) covers the period 1590 - 1990."
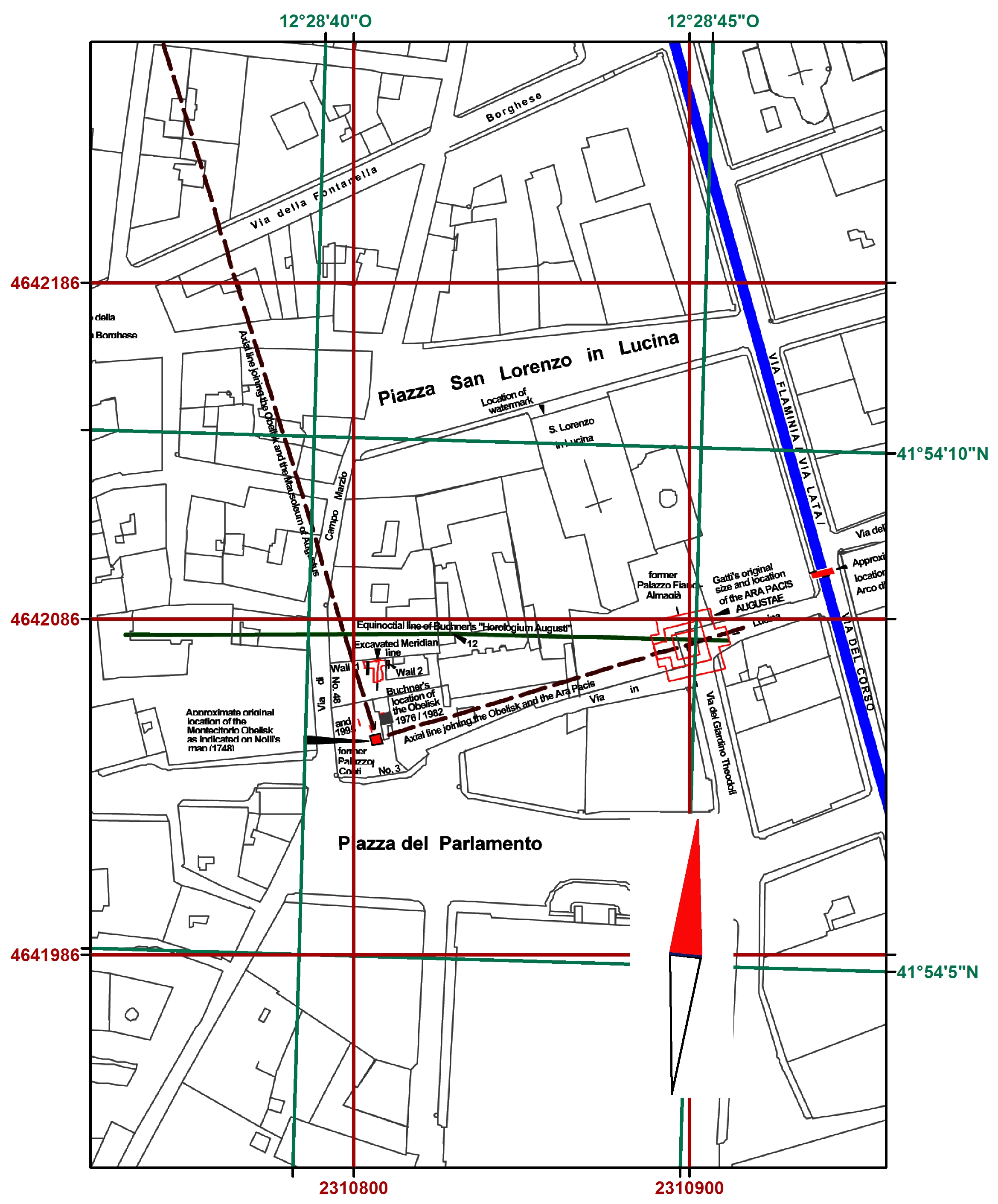
Abb. 6: Gitternord mit Gauss-Boaga Koordinaten und geographischen Koordinaten und magnetisch Nord, visualisiert mit einer Magnetnadel
(Die Magnetnadel des Kompasses ist gegenüber geographisch Nord, das durch die grünen Gitterlinien repräsentiert wird, leicht nach Osten geneigt und entspricht der aktuellen örtlichen Deklination für Rom von ca. 2,9°. Diese ändert sich aktuell jährlich um ca. 0,11°, modifizierte Abb. 4)
Der Pfeil in der Windrose auf der Karte von Nolli (vgl. Abb. 5) weist ebenfalls nach magnetisch Nord, jedoch zur Zeit Nolli's (1748), vgl. "Meridianus quem dat hodie Acus Magneticae" (BEVILAQUA 1998, S. 13)
Werden also Messungen von Himmelsrichtungen mit dem Kompass durchgeführt, ist insbesomdere [Korrektur: insbesondere] auf die Mißweisung/Deklination, also die Abweichung von der geographischen Nordrichtung zu achten. Ort gleicher Deklination/Mißweisung werden durch Isogonen dargestellt. Diese Isogonen werden auch als magnetische Meridiane bezeichnet (WAGNER 1971, S. 23). Im internationalen Flugverkehr werden für alle Flughäfen Daten zur magnetischen Deklination herausgegeben und ständig korrigiert. So beträgt der Wert für die beiden Flughäfen Roms "Leonardo da Vinci International Airport", ehemals "Fiumicino" FCO 2,87° (WMM 2015 magnetic declination with 0,11° annual change) und für "Ciampino" 2,93° (WMM 2015 magnetic declination with 0,11° annual change).
Geodaten und das Archäologische Informationssysteme AIS ROMA
Das Koordinatensystem im AIS ROMA entspricht dem der amtlichen photogrammetrischen Vektordaten (zu Vektordaten vgl. HÄUBER, SCHÜTZ 2004, S. 27-28) der Stadt Rom, also Gauss-Boaga (vgl. oben). Sämtliche Karten wurden und werden von Chrystina Häuber digital erstellt und sind daher grundsätzlich "Gitternord" orientiert (vgl. ihre Karten in diesem Band). Um diese Karten anzufertigen, wurden insbesonders kartographische Quellen zunächst in hoher Auflösung gescannt und sodann entzerrt und georeferenziert. Je nach Koordinatensystem der Quelle wurden verschiedene Verfahren zur möglichst passgenauen räumlichen Integration dieser Daten angewandt, wie Transformationen, Entzerrungen und Georeferenzierung.
WITTE, SPARLA 2015 definieren Photogrammetrie so: "Unter Photogrammetrie versteht man ein berührungsloses Messverfahren, bei dem aus photographisch gewonnenen Bildern durch deren Auswertung Form und räumliche Lage von Objekten bestimmt werden." (ebd., S. 339). Bei den von uns im AIS ROMA benutzten amtlichen Grunddaten handelt es sich um Vektordaten, die aus Luftbildern gewonnen wurden. Das SITAR (Sistema Informativo Territoriale Archeologico di Roma) basiert ebenfalls auf diesen amtlichen Daten, vgl. dazu ausführlich die Bände von SERLORENZI (2011) und SERLORENZI, JOVINE (2013). Die Photogrammetrie kann auf eine lange Geschichte zurückblicken. "In München beschäftigte man sich mit der Fotogrammetrie im Topographischen Büro des bayerischen Generalstabs ab dem Ende der 1880er Jahre. In regem Austausch standen die Offiziere des Topographischen Büros mit Sebastian Finsterwalder (1862-1951), der sich 1888 an der Technischen Hochschule habilitiert hatte und dessen besonderes Interesse in seinem weiten Tätigkeitsfeld der Fotogrammetrie galt" (LEIDEL, FRANZ 2006, S. 300). Mit "zwei aus einem Freiballon aufgenommenen Luftbildern hat er schon 1902 eine Karte aus der Gegend von Gars am Inn im Maßstab 1:10000 mit Höhenlinien konstruiert. Bei dieser Karte handelt es sich wohl um die erste am Luftbild orientierte kartographische Darstellung (LEIDEL, FRANZ 2006, S. 300).
Zu "Anwendungen des Luftbildwesens" (KONECNY, LEHMANN) und den Grundlagen insbesondere analoger photogrammetrischer Auswerteverfahren vgl. ausführlich bei KONECNY, LEHMANN, S. 324-335. Zu "Photogrammetrie und Kartographie", insbesondere einschließlich neuester Entwicklungen, wie beispielsweise "UAV-Photogrammetrie" (WITTE, SPARLA 2015, S. 386-398). UAV steht dabei für Unmanned Aerial Vehicle(s).
Anwendungsbeispiel 3/4-D Modellierung
Bei den bislang gezeigten Visualisierungen handelt es sich insbesondere um 2D-Visualisierungen (Karten), die mit dem AIS ROMA generiert wurden. Neben den im Forschungs- und Entwicklungsstadium befindlichen 3/4-Funktionalitäten des AIS ROMA, die vom Autor hauptsächlich in C/C++ und JAVA implementiert (programmiert) werden (vgl. SCHÜTZ 2015), existieren kommerziell verfügbare Softwarelösungen, die für 3/4D-Modellierungen in urbanen Räumen gut geeignet sind.
|
|
|
|
|
|
Abb. 7: Beispiel einer räumlich-temporalen (3/4D) Modellierung und Simulation
(Oben links: Digitales Geländemodell mit Tibermündung und photogrammetrischen Daten aus dem Marsfeld in Rom (rote Fläche etwa in der Bildmitte). Oben rechts: 3D-Simulation auf Grundlage photogrammetrischer Daten in Gauss-Boaga und unkorrigierter Oberflächendaten mit aktueller Bebauung. Unten: 3/4D-Simulation von Sonnenständen, aktuelle Situation, ohne Bebauung, schematische Darstellung ohne bestimmte Objektform und Objekthöhe und ohne bestimmte Sonnenstandswinkel. Erstellt vom Autor mit Esri CityEngine)
Seit 2012 arbeitet der Autor mit der Software CityEngine (CE) von Esri, mit der Abb. 7 angefertigt wurde. In Berührung mit dieser Software und mit der Software Unity kam ich durch meinen Kollegen an der Hochschule München, Professor Dr. Markus Oster, der sich seit langer Zeit mit interaktiver 3D-Visualisierung beschäftigt. Unsere erste gemeinsame Lehrveranstaltung mit Anwendung der Software CityEngine haben wir im Wintersemester 2012/13 im Masterstudiengang Geomatik durchgeführt. Wir haben die Idee der Kopplung von objektorientierten Datenbanken mit der CityEngine und Unity entwickelt, um die Vorteile der entsprechenden Softwarekomponenten, insbesondere für interaktive 3D-Modellierung in Echtzeit nutzen zu können. Erfolgversprechende Versuche haben wir bereits unter Anwendung des Esri CE SDK, Unity, db4o und der boost C++ library durchgeführt (vgl. zum Esri CityEngine SDK: https://github.com/Esri/esri-cityengine-sdk; es existiert dort auch ein "plugin" für Autodesk Maya). Ein Vorteil der CityEngine ist beispielsweise die Möglichkeit, auf der Grundlage von projizierten Geodaten, z.B. in Gauss-Boaga, zu arbeiten (vgl. Abb. 7), was in Unity grundsätzlich nicht möglich ist. Unity bietet dafür vielfältigste Möglichkeiten der schnellen interaktiven Visualisierung und Compilierung, auch für mobile Endgeräte.
FRISCHER hat im Projekt "Rome reborn" (vgl. WELLS, FRISCHER, ROSS, KELLER 2010) eine sehr frühe Version der Software benutzt, die inzwischen als Esri CityEngine weiterentwickelt wurde, ebenso benutzt er die Software Unity. Ich konnte seine aus Sicht der Geo-Medieninformatik sehr interessante Applikation anläßlich eines Vortrags von ihm am 3. Juli 2015 hier in München sehen. Aus Sicht der Altertumswissenschaften kann ich die Anwendung nicht beurteilen.
Will man nun 3/4D-Visualisierungen für die Vergangenheit durchführen, den aktuellen Zustand also gleichsam zurückschreiben, wären dafür bei Anwendung der CityEngine zumindest folgende Schritte notwendig: Laden von hochgenauen, amtlichen Referenzdaten im 2- und 3D-Bereich. Ermittlung und Integration der verschiedenen Oberflächenniveaus zum Zeitpunkt, der rekonstruiert werden soll. Bei Simulationen zusätzlich Rekonstruktion der auf der Oberfläche befindlichen Objekte, z.B. Bebauung, Straßen und Rückrechnung von Sonnen- und Wasserständen.
Zusammenfassung und Schlußfolgerungen
Der Beitrag hat den Versuch unternommen, die Begriffe "Meridian", "Orientierung", "Koordinatensysteme", "Norden", "Gitter" insbesondere im digitalen Kontext und im Kontext Archäologischer Informationssysteme in der gebotenen Kürze an Anwendungsbeispielen zu zeigen. Wir haben gesehen, dass heute mindestens vier verschiedene Nordrichtungen existieren, die es beim Versuch räumlich-temporaler Rekonstruktionen zu beachten gilt: Himmelsnord, geographisch Nord, Gitternord und magnetisch Nord. Des Weiteren existieren zahlreiche Koordinatensysteme mit den unterschiedlichsten Parametern, die bei einer Datenintegration unbedingt zu beachten sind. Selbst bei hochgenauen Transformationen (7-Parameter Transformation) von und in das Gauss-Boaga Koordinatensystem (z.B. Datumstransformation in ETRS89) ist mit Lageungenauigkeiten von ca. 3-4 Metern zu rechnen (MUGNIER 2005, S. 890).
Beispielsweise gestaltete sich der Versuch der Integration des Plans "Fig. 1" in LEONHARDT 2014, S. 102 als unerwartet problematisch. Sind Pläne bzw. Karten in sich homogen und konsistent, ergeben sich bei der Integration selbst bei der Verwendung von lediglich zwei Passpunkten über Distanzen von 700 Metern (z.B. bei Abb. 3) so gut wie keine Passungenauigkeiten mit den amtlichen Daten. In diesem Fall existierten jedoch bereits innerhalb einer vergleichsweise kleinen Fläche mir unerklärliche Passungenauigkeiten. Die Fehlerquellen dafür können in einem solchen Fall vielschichtig sein und von der "Vermischung" unterschiedlicher (kartographischer) Quellen (Karten und Pläne) mit unterschiedlichen Koordinatensystemen und Projektionen bis hin zum Druckverfahren reichen, wenn beispielsweise die Pläne nicht proportional gedruckt worden sind.
Ebenso können Fehler bei Messungen in am Bildschirm visualisierten bzw. ausgedruckten Karten und Plänen auftreten, obwohl diese mit winkel-, flächen- oder längentreuer Projektion angefertigt sind. Messungen am Bildschirm lassen sich geometrisch korrekt lediglich auf kalibrierten Bildschirmen durchführen. Im Labor für Medientechnik an der Hochschule München sind dazu hardwarekalibrierbare Bildschirme vorhanden. Viele Softwarepakete bieten zudem die Möglichkeit, Bildschirmproportionalitäten und Seitenverhältnisse korrekt und auf den entsprechenden Bildschirm einzustellen.
2/3/4D-Visualisierungen für die Vergangenheit in großem Maßstab, insbesondere für (aktuell) urbane Räume sind bereits im 2D-Bereich überaus zeitaufwendig. Es sollten zunächst räumlich valide 2D-Rekonstruktionen in einem möglicht genauen Koordinatensystem vorliegen, bevor mit dem Versuch von Rekonstruktionen in der dritten Dimension begonnen wird.
Appendix
Benutzte Informationssysteme, Software und digitale Grunddaten
AIS ROMA, Datenbestand vom Juli 2017
Esri ArcMap 10.1, Esri ArcGlobe 10.1 , Esri CityEngine 2014.0
Digitale photogrammetrische Daten der Comune di Roma (aktuell Roma Capitale) in
Gauss-Boaga
Parameter für eingestelltes "Coordinate System"
Roma 1940 Gauss Boaga Est/ WKID 1020937 Projection: Transverse_Mercator/ False_Easting: 2520000,0/ False_Northing: 0,0/ Central_Meridian: 15,0/ Scale_Factor: 0,9996/ Latitude_of_Origin: 0,0/ Linear Unit: Meter (1,0)/ Geographic Coordinate System: GCS_Roma_1940/ Angular Unit: Degree (0,0174532925199433)/ Prime Meridian: Greenwich (0,0)/ Datum: D_Roma_1940/ Spheroid: International_1924/ Semimajor Axis: 6378388,0/ Semiminor Axis: 6356911,946127947/ Inverse Flattening: 297,0.
Zitierte Literatur
BILL, Ralf (2016): Grundlagen der Geo-Informationssysteme. Berlin und Offenbach. 6., völlig neu bearb. und erw. Aufl.
BEVILACQUA, Mario (1998): Roma nel Secolo dei Lumi. Architettura erudizione scienza nella Pianta di G.B. Nolli «celebre geometra». Napoli.
CHRISTOPH, Andreas, AMMON, Michael, CROM, Wolfgang, PRZIBYTZIN, Holger (2016): Digitalisierung - Verortung - Recherche | Neue Perspektiven für historische Karten. In: Kartographische Nachrichten, Journal of Cartography and Geographic Information, 66. Jahrgang, April 2016, Heft 3, 3.2016, S. 115-122.
FLACKE, Werner, DIETRICH, Mareike, GRIWODZ, Uta, THOMSEN Birgit (2015): Koordinatensysteme in ArcGIS. Praxis der Transformationen und Projektionen Berlin, Offenbach. 3., neu bearb. Aufl.
FRISCHER, Bernard, CRAWFORD, Jane Webb, KOLLER, David (Edited by)(2010): Making History Interactive. Computer Applications and Quantitative Methods in Archaeology (CAA). Proceedings of the 37th International Conference, Williamsburg, Virginia, United States of America, March 22-26, 2009. BAR International Series 2079, 2010. Oxford
GULLIVER F.P. (1908): Orientation of Maps. In: Journal of Geography, 7:3, S. 55-58.
HÄUBER, Chrystina., SCHÜTZ, Franz Xaver (2004): Einführung in Archäologische Informationssysteme (AIS). Ein Methodenspektrum für Schule, Studium und Beruf mit Beispielen auf CD. Mainz am Rhein
HÄUBER, Chrystina (2014): The Eastern Part of the Mons Oppius in Rome: the Sanctuary of Isis et Serapis in Regio III, the Temples of Minerva Medica, Fortuna Virgo and Dea Syria, and the Horti of Maecenas. With Contributions by Edoardo Gautier di Confiengo and Daniela Velestino, 22. Suppl. BullCom. Roma.
LEONHARDT, Günther 2014, "Horologium and Mausoleum Augusti: an overview of the fieldwork (1979-97) and the existing documentation", in: Haselberger, Lothar 2014, The Horologium of Augustus: Debate and Context, 99. Suppl. JRA. S. 101-106.
JENSCH, Georg (1970): DIE ERDE und ihre Darstellung im Kartenbild. Braunschweig.
KAIBEL, Georg (1885): Antike Windrosen. In: Hermes: Zeitschrift für klassische Philologie. Band 20, S. 579-624.
KONECNY, Gottfried, LEHMANN, Gerhard (1984): Photogrammetrie. Berlin, New York. 4., völlig neu bearb. Aufl.
LEIDEL, Gerhard unter Mitarbeit von Monika Ruth Franz (2006): Von der gemalten Landschaft zum vermessenen Land. Eine Ausstellung des Bayerischen Hauptstaatsarchivs zur Geschichte der handgezeichneten Karte in Bayern. Ausstellungskatalog. München.
MUGNIER, Clifford J. (2005): Grid & Datums. Italian Republic. In: Photogrammetric Engineering & Remote Sensing, August 2005, S. 889-890.
MURAWSKI, Hans (1977): Geologisches Wörterbuch. Stuttgart. 7., erg. und erw. Aufl.
PEITZ, Adolf (1978): Sonnenuhren 2. Tabellen und Diagramme zur Berechnung. München.
RÖSLER, Hans Jürgen (1991): Lehrbuch der Mineralogie. Leipzig. 5., unv. Aufl.
ROHR, René R.J. (1982): Die Sonnenuhr. Geschichte Theorie Funktion. München.
SCHÖDLBAUER, Albert (2000): Geodätische Astronomie. Grundlagen und Konzepte. Berlin, New York.
SCHÜTZ, Franz Xaver 2015, "Why work with geographers in reconstructions and visualizations of ancient Rome? An application of the landscape(t)-model" (online version). URN: http://nbn-resolving.de/urn/resolver.pl?urn=nbn:de:bvb:19-epub-25173-5
SCHUMACHER, Heinz (1978): Sonnenuhren 1. Eine Anleitung für Handwerk und Liebhaber. Gestaltung, Konstruktion, Ausführung. München. 2. Aufl.
SERLORENZI, Mirella (a cura di)(2011): SITAR. Sistema Informativo Territoriale Archeologico di Roma. Atti del Convegno, Roma 26 ottobre 2010. Roma
SERLORENZI, Mirella e JOVINE, Ilaria (a cura di)(2013): SITAR. Sistema Informativo Territoriale Archeologico di Roma. Atti del II Convegno, Roma 9 novembre 2011. Roma.
STRAHLER, Arthur N. (1973): Introduction to Physical Geography. New York et al. Third Edition.
THIEL, Rudolf (1956): Und es ward Licht. Roman der Weltallforschung. Berlin und Darmstadt. (Nachdruck 1958).
WAGNER, Julius (1971): Physische Geographie. München u.a. 6. Aufl. (= Harms Handbuch der Erdkunde, Bd. VIII).
WELLS, Sarah, FRISCHER, Bernard, ROSS, Doug, KELLER, Chad (2010): Rome Reborn in Google Earth. In: FRISCHER et al. 2010, Oxford et al., BAR International Series 2079, S. 373-379 (S. 365-371 auf CD-ROM)
WITTE, Bertold, SPARLA, Peter (2015): Vermessungskunde und Grundlagen der Statistik für das Bauwesen. 8., neu bearb. und erw. Aufl.
Folgenden Personen und Institutionen, die durch vielfältige Hilfe und Unterstützung zum Entstehen und Gelingen meines Textes beigetragen haben, gilt mein aufrichtiger Dank: Johann Anderl (†), Ursula Hoffmann, Kurt Lehr, Markus Oster, Eugenio La Rocca, Claudio Parisi Presicce, meiner Frau Chrystina Häuber, dem FORTVNA Research Center for Archaeological Information Systems Regensburg, München und der Hochschule München.
Fussnote 1 Prof. Eugenio La Rocca, zu dieser Zeit Sovraintendente ai Beni Culturali der Comune di Roma hatte uns (Dr. Chrystina Häuber und dem Autor) diese Daten erstmals im März 1999 zur Verfügung gestellt. Im Februar 2014 hat der Sovraintendente ai Beni Culturali von Roma Capitale, Dr. Claudio Parisi Presicce unsere Kooperationsvereinbarung erneuert. Diese beinhaltet auch die Genehmigung zur Veröffentlichung der mit unter Verwendung der amtlichen photogrammetrischen Daten angefertigten Karten. Dafür danke ich beiden Personen sehr herzlich, ebenso (seit 2004 meiner Ehefrau) Chrystina Häuber für die immerwährende Unterstützung und die Überlassung der von ihr angefertigten Rekonstruktionen, insbesondere in Karten zur antiken Topographie der Stadt Rom, die ebenfalls die photogrammetrischen Daten als grundsätzliche räumliche Referenz verwenden.
Autor:
Franz Xaver Schütz
Professor Dr. phil. rer. nat. habil.
Hochschule München / University of Applied Sciences Munich
Fakultät für Geoinformation / Fachgebiet: Geo-Medieninformatik
(Stand: 2017)
Datenschutzerklärung | Impressum